SAR成像几何及回波信号
条带模式成像几何
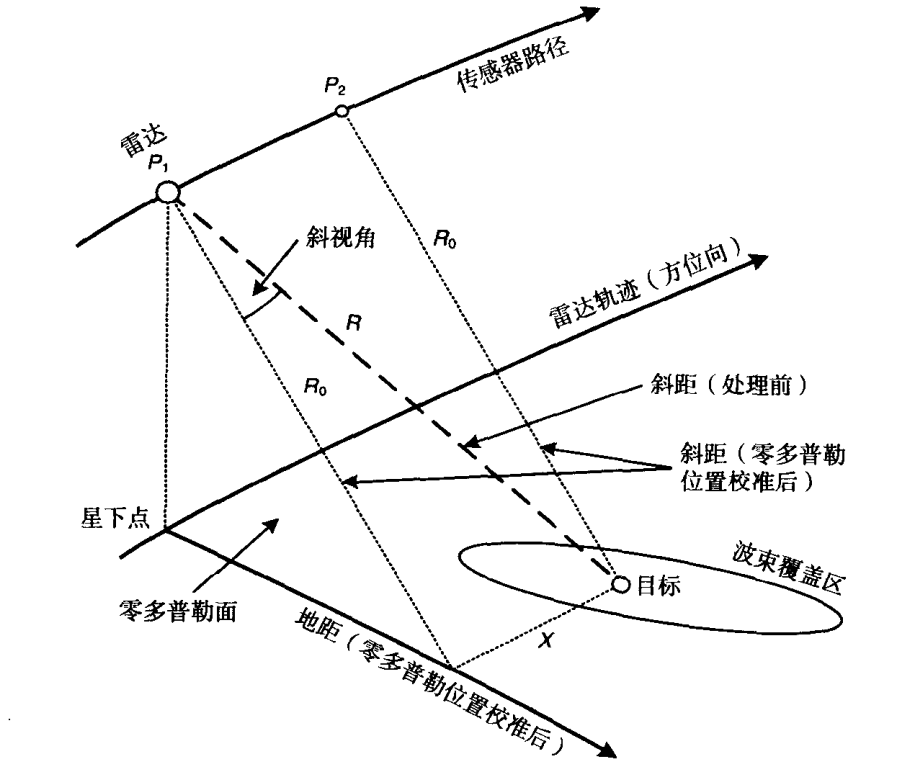
我们使用如下图所示的几何关系来描述SAR成像
名词解释
目标: 我们使用理想的点目标来建立SAR成像的几何关系,这样的点目标称为点散射体。
波束覆盖区: 即当雷达发射某个脉冲时,雷达天线波束投影到地面的区域,波束覆盖区的位置与形状同波束方向图及雷达几何关系相关。
星下点: 位于传感器正下方的地表位置点
雷达轨迹: 星下点在地表的移动轨迹
距离向: 在SAR成像几何中,距离可以指斜距或地距,散射体的斜距即沿雷达视线方向的距离,而地距指将斜距投影到地面上的距离,通常来说距离向指的就是雷达视线方向
方位向: 即雷达速度的方向
零多普勒面: 即垂直于雷达速度方向的平面,由多普勒频率的定义可知,在该平面上的点多普勒频率均为0,因此称为零多普勒面,由几何关系容易知道,零多普勒面经过目标的时刻,目标与雷达间的距离达到最短,该时刻称零多普勒时刻
波束宽度: 雷达波束可以看成一个圆锥体,而波束覆盖区就是雷达波束与地面的相交的区域,波束宽度指的是天线辐射强度相比峰值点降低3dB的位置之间的夹角。
- 在方位向上,天线激励认为是均匀的,则波束宽度认为等于波长除以方位向的天线长度,即$\beta=0.886\lambda/L$
- 在俯仰向上,波束宽度决定了成像区域在地距上的范围,也就是距离向成像宽度
斜视角: 斜视角是在斜距平面(雷达速度矢量和斜距矢量构成的平面)内雷达波束中心和零多普勒面的夹角,斜视角对成像的影响很大。 波束中心穿越时刻: 由于斜视角的存在,使得波束中心穿越目标的时刻并不一定为零多普勒面穿越目标的时刻,此外,当斜视角存在时,和距离向垂直的不再是方位向,此时称距离横向。
距离向信号
在脉冲压缩中已经提到了,雷达发射的信号为线性调频信号,其表达式为
\(\begin{align}
s(t) = \mathrm{rect} \left[ \frac{t}{T_p} \right] \cos \left( 2\pi f_c t+\pi K_r t^2 \right)
\tag{1}
\end{align}\)
回波信号为发射信号与目标散射系数$g(t)$的卷积,设距雷达$R_0$处一点目标的后向散射系数$\sigma_0$的幅度为$A_0$,则回波信号为
\(\begin{align}
s_r(t) &= s(t) \otimes g(t) \\
&= s(t) \otimes A_0 \delta(t-\frac{2R_0}{c}) \\
&= A_0* \mathrm{rect} \left[ \frac{t-2R_0/c}{T_p} \right] \cos \left( 2\pi f_c (t-\frac{2R_0}{c})+\pi K_r (t-\frac{2R_0}{c})^2 + \psi\right)
\tag{2}
\end{align}\)
其中$\psi$表示散射过程中引起的额外相位。
方位向信号
多普勒频率
雷达在运动过程中,速度和斜距的夹角不可能时刻垂直,从而雷达有和目标连线方向上的速度,而这个就会产生多普勒频率,设雷达速度在斜距向的投影值为$v_r$,当雷达接近目标时,目标作为观察者接收的频率为$f^{‘}=\frac{c}{c-v_r}f$,频率增量$\Delta f \approx \frac{v_r}{\lambda}$,反射的回波雷达作为观察者再经历一次频率增加,由此雷达信号处理中的多普勒频偏量可以表示为$f=\pm \frac{2v_r}{\lambda}$,接近为正,远离为负。
方位向历程
为了简化分析,将成像几何简化为在斜距平面内,如下图所示
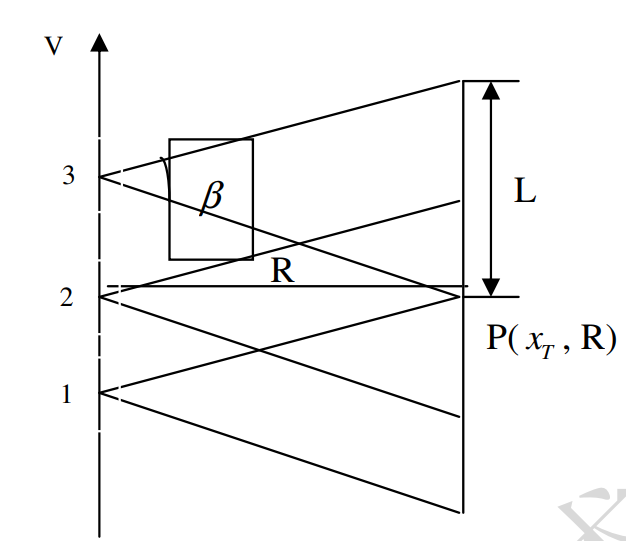
距离向回波信号的存在时间的决定于脉冲时长和回波时延,而方位向上,有无雷达信号取决于波束是否照射到目标,为了分析方便,我们设零多普勒时刻为时间起点,最短斜距为$R_0$,则目标到雷达的斜距为$R(\eta)=\sqrt{R_{0}^{2}+(v\eta)^2}$。当该斜距连线在波束范围内时即为雷达照射到目标,设全照射过程中雷达运动距离$L_a$ ,波束宽度$\beta$,则近似有$L_a=R_0\beta$
可以看到即使在波束宽度内,信号强度也会发生变化,但为了分析方便我们认为波束宽度内强度均为常数。
几个重要参数
波束中心穿越时刻: 在零多普勒时刻为时间起点的情况下,设斜视角为$\theta$,则波束中心穿越时刻为$\eta_c=\pm \frac{R_0 \tan{\theta}}{v}$,斜视角前视为正,后视为负。
多普勒中心频率: 波束中心穿越时刻的多普勒频率,容易得到$f=\frac{2v\sin{\theta}}{\lambda}$。
多普勒带宽: 随着雷达的运动,雷达先接近目标再远离,因此多普勒频率先正后负,因此具备一个带宽,此多普勒带宽的计算方式为$BW=\frac{2v\beta}{\lambda}\cos{\theta}$。
方位向信号
我们称$t$为快时间或距离向时间,以每个脉冲的发射时刻为0时刻,衡量脉冲在距离向上的飞行时长。$\eta$为慢时间或方位向时间,衡量各个脉冲的发射时刻,由上面的分析我们得到一个点目标在雷达飞行的全过程中回波信号的表达式为
\(\begin{align}
s_r(t,\eta) &= A_0* \mathrm{rect} \left[ \frac{t-2R_0/c}{T_p} \right]*\mathrm{rect} \left[ \frac{\eta-\eta_c}{L_a/v} \right] * \\
&\cos \left( 2\pi f_c (t-\frac{2R(\eta)}{c}) + \pi K_r (t-\frac{2R(\eta)}{c})^2 + \psi\right)
\tag{3}
\end{align}\)
正交解调后的基带信号表达式为(不考虑幅度$A_0$及附加相位$\psi$)
\(\begin{align}
s_r(t,\eta) &= \mathrm{rect} \left[ \frac{t-2R_0/c}{T_p} \right]*\mathrm{rect} \left[ \frac{\eta-\eta_c}{L_a/v} \right] * \\
&e^{j\pi K_r (t-\frac{2R(\eta)}{c})^2} e^{-j4\pi f_c R(\eta)/c}
\tag{4}
\end{align}\)