脉冲压缩
线性调频信号
线性调频信号(LFM信号或chirp信号)是指瞬时频率随时间成线性变化的信号。在一个脉冲内的LFM信号时域表达式可以写为(通常我们用复数形式表示)
\[\begin{align} s(t) = \mathrm{rect} \left[ \frac{t}{T} \right] e^{ j\pi kt^2 } \tag{1} \end{align}\]$\mathrm{rect}$函数定义为
\[\begin{align} rect \left[ \frac{t}{T} \right]= \left\{ \begin{array}{lr} 1, & |t| < T/2 \\ 0, & otherwise \\ \end{array} \right. \tag{2} \end{align}\]其中$T$为脉冲持续时间,$k$为线性调频率,单位$\mathrm{Hz}/s$,其实部虚部及频谱相位如下图所示
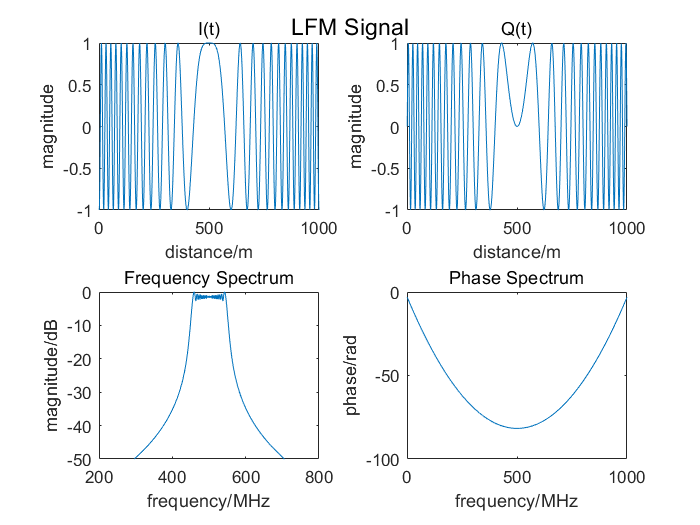
对其进行分析可得信号的相位$\phi(t)=\pi kt^2$,对其求导得到频率为$f=kt$,这也是chirp信号称做线性调频信号的原因,由于其持续时间为$T$,因此信号带宽为$B=kT$。
在雷达信号处理中,时间带宽积$TBP$是一个很重要的概念,它表示一个信号带宽和时长的乘积,最传统的矩形脉冲其频谱为sinc函数,因此其TBP约为1,同时这也是物理可实现信号中几乎最低的TBP。而线性调频信号的TBP为$kT_{p}^{2}$
线性调频信号相比于传统的矩形脉冲来说突出的优点就在于,其时长和带宽具备一定的独立性,在矩形脉冲中,其TBP近似为1,为常数。这就说明我们在增加其脉冲时长时就会减小带宽,TBP保持不变。而Chirp信号的带宽和时长通过可调的调频率$k$联系起来,这就说明我们可以相对独立地调整时长$T_p$和带宽$B$。在后面可以看到,这种可调的TBP正是实现脉冲压缩的关键。
脉冲压缩
对于一个矩形脉冲来说,其时间分辨率为$\rho=T$,即两个回波脉冲的间距若小于其时长就会混叠在一起,导致无法将它们区分出来。因此,我们要获得高分辨率就需要缩短时长,但短时长的信号意味着能量低,雷达回波的信噪比将严重恶化。虽然高峰值功率的脉冲可以一定程度上弥补这个问题,但通常来说我们还是通过延长发射时间来提高回波的信噪比。
脉冲压缩技术就是为了解决此信噪比和分辨率的矛盾,其完整过程为首先发射一大时宽的信号,随后在收到回波之后对其进行处理,使得脉冲被压缩为一短时宽(即高分辨)的信号,这个过程即为脉冲压缩。
在雷达信号处理中,脉冲压缩通过匹配滤波来实现,我们首先通过一个例子介绍整个流程,再加以分析。
实例
参数
| 参数 | 代号 | 数值 |
|---|---|---|
| 脉冲持续时间 | $T_p$ | $10\mu s$ |
| 载频 | $f_c$ | $10GHz$ |
| 信号带宽 | $B$ | $10MHz$ |
| 采样率 | $f_s$ | $100MHz$ |
| 目标距离 | $R$ | $3000m$ |
分析仿真
由已知参数可知,雷达波从发射到返回的回波时延为$t_0=\frac{2R}{c}$,则回波信号可以表示为
\(s_r(t)=\mathrm{rect} \left[ \frac{t-t_0}{T_p} \right] e^{ j\pi (2f_c(t-t_0)+k(t-t_0)^2) } \tag{3}\) 信号经正交解调去载频后得到的基带信号为 \(s_r(t)=\mathrm{rect} \left[ \frac{t-t_0}{T_p} \right] e^{ j\pi k(t-t_0)^2}e^{-j4\pi f_cR/c} \tag{4}\) 如下图所示
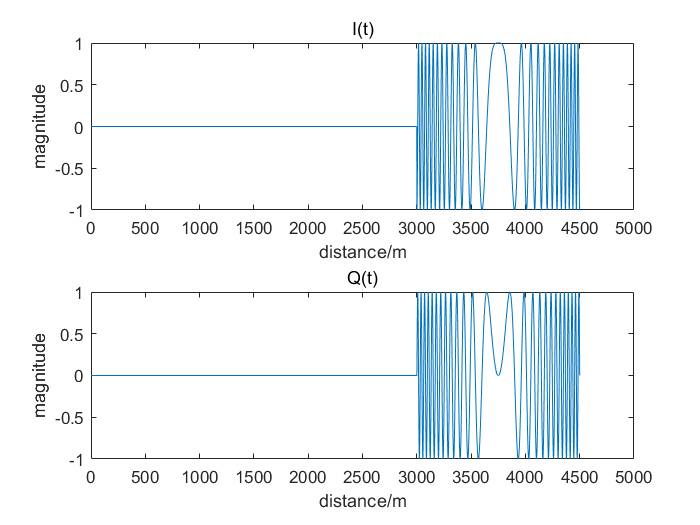
构造匹配滤波器需要参考信号,在脉冲压缩中,参考信号由发射信号$s(t)$复制而来,又称为复制信号,由匹配滤波器定义我们有
\(h(t) = s^{*}(-t)
\tag{5}\)
通常我们在频域构建匹配滤波器,由傅里叶变换的性质我们知道$\mathcal{F}[x^{}(-t)]=X^{}(\omega)$,由此匹配滤波器构建由下述步骤进行
- 将复制信号(即发射信号)补0至和回波信号等长(可以都补0至某一点数)
- 将回波信号的傅里叶变换$S_r(\omega)$与复制信号的傅里叶变换的复共轭$S^{*}(\omega)$相乘
- 对结果做逆傅里叶变换即得到滤波结果
在不考虑相位项$e^{-j4\pi f_cR/c}$的情况下我们得到匹配滤波结果为
\(\begin{align}
s_{out}(t) & =s_r(t) \otimes h(t) \\
& \approx T_p* \mathrm{sinc}(kT_p(t-t_0))
\tag{6}
\end{align}\)
结果如下图所示
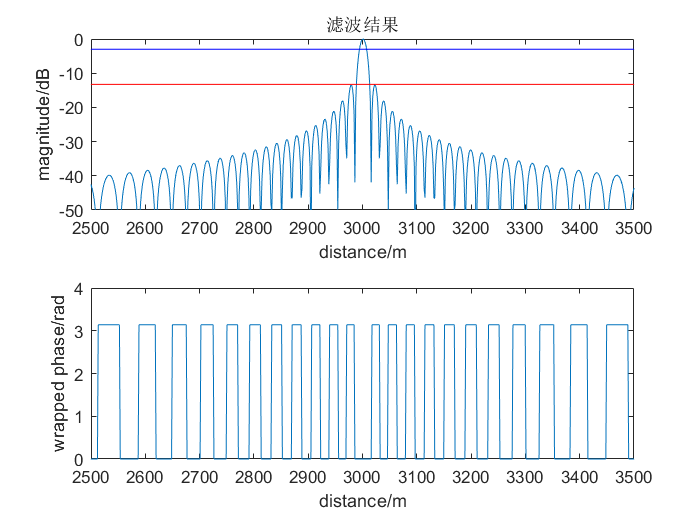
结果分析
我们可以看到,匹配滤波将输入的Chirp信号处理成了近似sinc函数的形式,从sinc函数的特点我们可以知道,其时间轴的主瓣3dB宽度即其分辨率,约为$\rho^{‘}=0.886/B$,在实际使用时有时也使用sinc函数的第一零点作为时间分辨率的临界值,此时为$\rho^{‘}=1/B$。相比脉冲压缩前分辨率$\rho=T_p$有了很大提升,为了衡量这个压缩效果,我们定义压缩比$C$为
\[\begin{align} C=\frac{\rho}{\rho^{'}} \approx |k|T_{p}^{2} \tag{7} \end{align}\]我们可以从下面这个角度来理解脉冲压缩。
由于匹配滤波的滤波器形式是由信号波形得到的,因此滤波器与信号具有相同的带宽,但由于取了共轭因此相位相反,因此匹配滤波不改变带宽,同时将相位处理为常数(或线性相位),同时由于Chirp信号频谱在自身的带宽内近似为常数,因此匹配滤波的输出结果为一频率幅度谱近似为门函数,相位常数或线性的信号,这正是sinc函数的频谱特征,因此使用线性调频信号,我们可以在匹配滤波时将Chirp信号在不改变带宽的情况下压缩为近似TBP最小的sinc函数形式的信号,因此其时间分辨率得到了极大地提高,这就是所谓脉冲压缩。
此外,匹配滤波可以理解为信号自身的自相关,那么当回波信号与复制信号进行匹配滤波时就相当于衡量两者的相似程度,只有复制信号平移至与回波信号对齐时两者最相似,同时由于取共轭消除了幅角的影响,此时信号完全与自身相干叠加,因此滤波结果相当于将分散在各时间点的能量“聚集”在了回波信号起始位置,因此这种能量的聚集使得分辨率得以提高。
一个问题
在仿真时发现一个问题,即当对Chirp信号进行取样时,对信号时间域采样在$(0:N-1)/N*T_p-T_p/2$进行取样与$linspace(-T_p/2,T_p/2,N)$方式进行取样,其相位会有略微的不同,如下图所示(上、下图对应前、后两种方式)
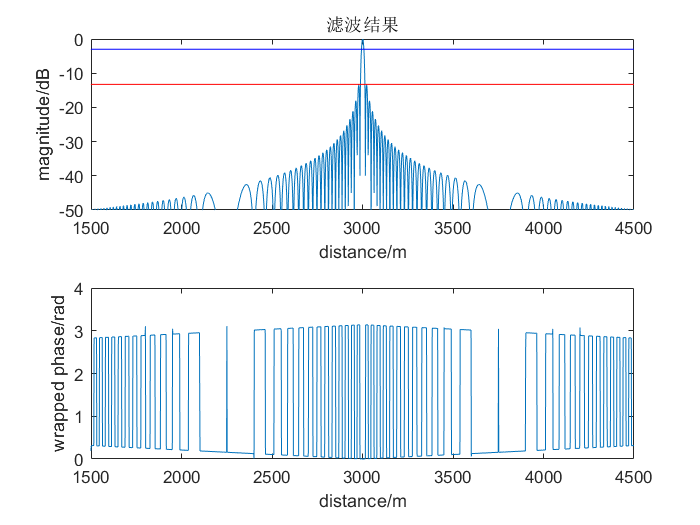

即前者产生了一个多余的线性相位,目前怀疑是前者的取样方式会使得取样部分的中心频率略微偏离零频产生的线性相位,但目前由于实验室很多人没有特别关注脉冲压缩在相位方面的特点,因此也没有一个特别权威的解答。
参考文献
Ian G.cumming等 合成孔径雷达算法与实现[M].